fisica

TEMA: VECTORES: QUE SON : 

En matemática y física, un vector^a​ es cualquier ente matemático que se puede representar mediante un segmento de recta orientado dentro del espacio euclidiano.

Un vector con un origen fijado queda determinado a partir de dos elementos:

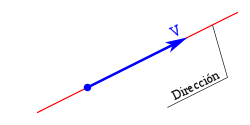
• Una semirrecta a partir de dicho origen, es decir, una dirección hacia la que apunta.^b​
• Un número no negativo, llamado módulo del vector y que mide su tamaño.

Alternativamente, se puede fijar un sistema de coordenadas del espacio ${\displaystyle �}$-dimensional; entonces un vector queda unívocamente determinado mediante ${\displaystyle �}$ números, llamados coordenadas del vector. El ejemplo más sencillo son las coordenadas cartesianas, un sistema de ${\displaystyle �}$ ejes reglados que se suelen tomar perpendiculares entre sí.

Así, fijado un sistema de ejes cartesianos —en otras palabras, un punto origen y una base— un vector tridimensional queda completamente determinado por tres números, llamados coordenadas cartesianas. Más concretamente, dados tres números ${\displaystyle (�,�,�)}$ se puede trazar una flecha o vector siguiendo estos pasos:

1. Desplazarse ${\displaystyle �}$ unidades en la dirección del eje ${\displaystyle �}$.
2. Desplazarse ${\displaystyle �}$ unidades en la dirección del eje ${\displaystyle �}$.
3. Desplazarse ${\displaystyle �}$ unidades en la dirección del eje ${\displaystyle �}$.
4. Trazar la flecha desde el punto origen hasta el de llegada.

• La velocidad de un automóvil. No sería suficiente describirla con tan solo un número, que es lo que marca el velocímetro, sino que se requiere indicar la dirección (hacia donde se dirige).
• La fuerza que actúa sobre un objeto, ya que su efecto depende, además de su magnitud o módulo, de la dirección en la que actúa.
• El desplazamiento de un objeto, pues es necesario definir la distancia que recorre, y la dirección del movimiento, o bien la posición inicial y final del objeto.

Definición[editar]

Componentes de un vector.

Un vector es un elemento de un espacio vectorial. En la práctica, cuando se tratan con vectores usualmente se expresan a una base vectorial. Así fijada un espacio vectorial específico y una base dentro del mismo:

Un vector (real) de dimensión ${\displaystyle �}$ viene representado por una tupla de números reales (que se llaman componentes del vector). El conjunto de todos los vectores de dimensión ${\displaystyle �}$ se representa como ${\displaystyle {\mathbb{�}}^{�}}$ (formado mediante el producto cartesiano). Así, un vector ${\displaystyle �}$ perteneciente a un espacio ${\displaystyle {\mathbb{�}}^{�}}$ se representa como:

${\displaystyle �=({�}_1,{�}_2,{�}_3,\dots ,{�}_{�})}$, donde ${\displaystyle �\in {\mathbb{�}}^{�}}$

El módulo o amplitud con una longitud proporcional al valor del vector. operaciones matrices (tales como el cambio de base), del modo siguiente:

${\displaystyle \mathbf{�}=\left[\begin{array}{c}{�}_{�}\\ {�}_{�}\\ {�}_{�}\end{array}\right]\mathbf{�}=[{�}_{�}{�}_{�}{�}_{�}]}$

Por ejemplo, los vectores unitarios se expresarían de la siguiente manera:

${\displaystyle \mathbf{�}=[100],\mathbf{�}=[010],\mathbf{�}=[001]}$

El lema de Zorn, consecuencia del axioma de elección, permite establecer que todo espacio vectorial admite una base vectorial, por lo que todo vector es representable como el producto de unos componentes respecto a dicha base. Dado un vector, solamente existen un número finito de componentes diferentes de cero.

CARACTERISTICAS

Los vectores, representados gráficamente, poseen las siguientes características:

• Dirección. Definida como la recta sobre la cual se traza el vector, continuada infinitamente en el espacio.
• Módulo o amplitud. La longitud gráfica que equivale, dentro de un plano, a la magnitud del vector expresada numéricamente.
• Sentido. Representado por la punta de la flecha que gráficamente representa al vector, indica el lugar geométrico hacia el cual se dirige el vector.
• Punto de aplicación. Correspondiente al lugar o punto geométrico en donde inicia el vector gráficamente.
• Nombre o denominación. Representado mediante una letra que acompaña al vector gráficamente representado, y que coincide con la magnitud que expresa o con la suma de los puntos de inicio y fin de su valor.

TIPOS

Según la ubicación de su punto de aplicación, los vectores se clasifican en:

• Vectores libres. Aquellos que no poseen un punto de aplicación particular.
• Vectores deslizantes. Aquellos cuyo punto de aplicación puede ser uno cualquiera a lo largo de la recta de aplicación.
• Vectores fijos o ligados. Aquellos que poseen un único y determinado punto de aplicación.

Sin embargo, también es posible clasificar los vectores según otros elementos, de la siguiente manera:

• Vectores angulares o concurrentes. Aquellos que forman ángulos respecto de sus líneas de acción o direcciones.
• Vectores opuestos. Aquellos que poseen igual magnitud pero sentido contrario.
• Vectores colineales. Aquellos que comparten recta de acción.
• Vectores paralelos. Aquellos cuyas líneas de acción sean, justamente, paralelas.
• Vectores coplanarios. Aquellos cuyas rectas de acción estén situadas en un mismo plano.

CALCULOS CON VECTORES

Suma de vectores

 

Si tenemos dos vectores  y , entonces la suma de  y  es

 

 

En otras palabras, el vector suma de  y  es el vector que resulta de sumar las componentes respectivas de estos vectores: la primera componente de  se suma con la primera componente de , y la segunda componente de  se suma con la segunda componente de .

 Interpretación gráfica de la suma

 

Observemos la siguiente gráfica que muestra la suma de los vectores  y :

 

Observa la siguiente figura que muestra la regla del paralelogramo.

 

 

Resta de vectores

 

La resta de dos vectores  y  simplemente es la suma de  con  (es decir, el opuesto de ).

 

De este modo, si consideramos los componentes de  y , entonces la resta está dada por

 

 

Gráficamente, la resta de  y  se obtiene igual que la suma. La única diferencia es que sumamos el opuesto de . Observa la siguiente figura que muestra a  y nota que en el extremo de  se coloca el origen de .

 

 

Observemos que la resta  gráficamente es el vector que une el extremo de  con el extremo de  tal y como se puede apreciar en la siguiente figura:

 

Producto de vector por escalar

 

La multiplicación de un vector  por un número  se escribe  o . El número  también se conoce como escalar. Además, la multiplicación por escalar es otro vector que satisface las siguientes propiedades:

 

•  tiene la misma dirección que .
• Si  es positivo, entonces  tiene el mismo sentido que .
• Si  es negativo, entonces  tiene el sentido contrario que .
• El módulo de  es 

 

Observemos la siguiente figura que representa la multiplicación de  por 3.

 

 

En términos de componentes, si , entonces la multiplicación por escalar está dada por

 

 

Ejemplos de ejercicios con vectores

 

Consideremos los vectores  y . Entonces:

 

1 La suma está dada por:

 

 

2 La resta es:

 

 

3 El opuesto de  es:

 

 

4 El producto escalar de  por 3 está dado por:

 

 

vectores